1.3 Das Künstliche Neuronale Netz

Bild generiert mit Ideogram 1.0 auf ideogram.ai

Einführung in Künstliche Neuronale Netze

Während das Perzeptron (wie in meinem letzten Abschnitt 1.2 Das Perzeptron erklärt) ein einzelnes Neuron im Gehirn modelliert, ist ein Künstliches Neuronales Netz (KNN) vergleichbar mit einem ganzen Netzwerk von Neuronen – daher der Begriff Netz(werk). Ich werde die Begriffe "Neuronales Netz" und "Künstliches Neuronales Netz" synonym verwenden.

Neuronale Netze können in ihrer Größe stark variieren, gemessen an der Anzahl der Parameter (Gewichte und Biases), die sie enthalten. Diese kann von Hunderten bis zu Billionen von Parametern reichen! Die Anzahl der Parameter bestimmt die Komplexität des Netzes und seine Fähigkeit, Muster zu lernen, die in den Trainingsdaten vorhanden sind. Die Gewichte bestimmen, wie beim Perzeptron erklärt, die Wichtigkeit der Eingabe, die ein Neuron erhält, während der Bias eine zusätzliche Ebene der Komplexität in das neuronale Netz einbringt, um die Trainingsdaten zu erlernen.

"Neuronales Netz" ist eigentlich ein Oberbegriff, der sich auf viele verschiedene Arten von neuronalen Netzwerkarchitekturen bezieht, jede mit eigenen Funktionsmechanismen und Anwendungsfällen. Hier ist ein grober Überblick:

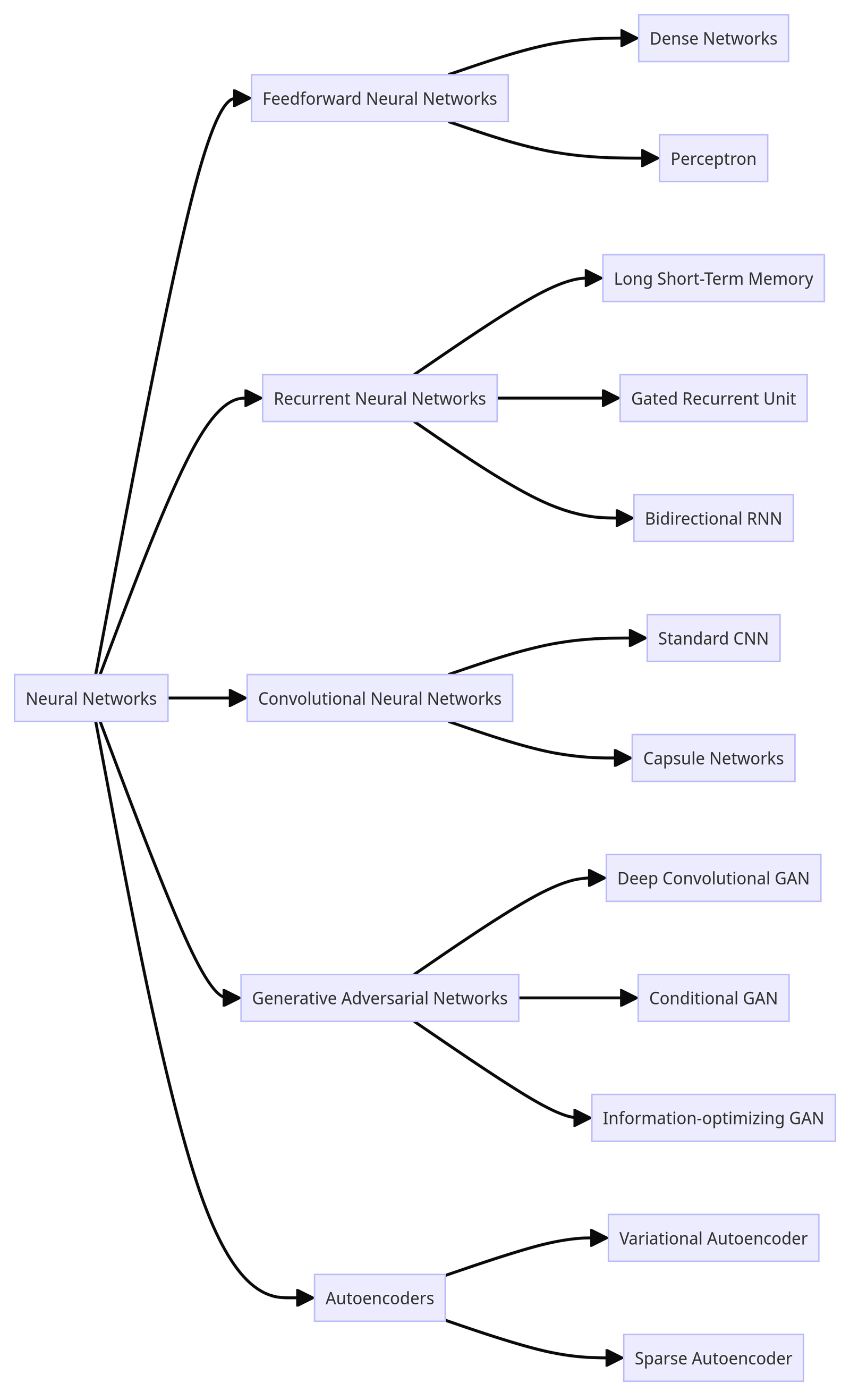
Abbildung 1: Diagramm der Architekturen neuronaler Netze

Wie du sehen kannst, gibt es eine große Vielfalt an neuronalen Netzen. Um im Kontext interaktiver KI-Chatbots (wie ChatGPT) zu bleiben, werden wir uns nur auf das Feedforward Neural Network (FNN) konzentrieren, insbesondere auf das Dense Network (auch bekannt als Fully Connected Neural Network oder Multilayer Perceptron).

Das FNN besteht aus einer riesigen Anzahl von "Perzeptron-Neuronen". Wenn du es noch nicht getan hast, empfehle ich dir dringend, den vorherigen Abschnitt 1.2 Das Perzeptron zu lesen, da er dir die notwendige Grundlage für das Verständnis des FNN liefert, über das wir jetzt sprechen werden.

In einem Feedforward-Neuronalen Netz wird die Information von der Eingabeschicht über die versteckten Schichten zur Ausgabeschicht ohne Schleifen verarbeitet. Die Information bewegt sich nur "vorwärts" durch das NN. Das Dense Network hat seinen Namen daher, dass jedes Neuron in einer gegebenen Schicht mit jedem Neuron in der nachfolgenden Schicht verbunden ist, daher die Bezeichnungen "dense" (dicht) oder "fully connected" (vollständig verbunden).

Struktur eines Feedforward Neuronalen Netzes

Anstatt des Regenschirm-Beispiels in 1.2 Das Perzeptron, werden wir ein viel komplexeres (und tatsächlich nützlicheres) Beispiel verwenden: das Erkennen einer gezeichneten Zahl zwischen 0 und 9 auf einem 28 × 28 Raster.

Die Eingabeschicht

Zunächst müssen wir überlegen, wie ein Bild in Zahlen dargestellt werden kann, da ein neuronales Netz nur mit numerischen Werten arbeiten kann. Dafür verwenden wir einfach ein Merkmal für jedes Pixel und nutzen den Graustufenwert jedes Pixels als Eingabe.

Wir haben 28 × 28 = 784 Pixel und somit 784 Eingabemerkmale. In der Eingabeschicht hast du Merkmale und keine Neuronen, weil Neuronen die Verarbeitungseinheiten sind, die Berechnungen mit den Eingabedaten durchführen. Die Eingabeschicht hält im Gegensatz zu den anderen Schichten einfach die rohen Eingabewerte, ohne Berechnungen durchzuführen. Der Graustufenwert liegt zwischen 0 und 1, wobei 0 weiß und 1 schwarz ist. 0.5 wäre ein perfektes Grau. Wie du siehst, ist das bereits viel mehr Eingabemerkmale, als die drei wir beim Perzeptron genutzt haben.

Die Versteckten Schichten

Hier geschieht der ganze Zauber der künstlichen Intelligenz (oder sollte ich sagen, hier passiert die ganze Mathematik?!) und hier lernt das neuronale Netz komplexe Muster. Technisch gesehen gibt es keine Grenze für die Anzahl der versteckten Schichten, aber manchmal ist weniger mehr. Diese versteckten Schichten extrahieren Muster aus den Trainingsdaten mit dem Ziel, diese erlernten Muster dann in einem gegebenen Eingabebild zu erkennen. Denk darüber nach, wie du eine Zahl erkennen würdest. Du würdest vielleicht nach Kreisen und Strichen suchen. Die Zahl "8" hat zum Beispiel einen Kreis auf einem anderen Kreis, während die "1" einen vertikalen Strich und einen kurzen diagonalen Strich hat, der von oben nach links unten verläuft. Wenn diese Muster während des Trainings korrekt gelernt würden (auch wenn wir uns dessen nicht bewusst sind), könnte KI eine menschliche oder sogar übermenschliche Leistung erreichen!

Hier liegt auch die Ähnlichkeit zum Perzeptron. Jedes Neuron in der versteckten Schicht erhält die Eingaben von jedem Neuron der vorherigen Schicht (in diesem Fall der Eingabeschicht), berechnet die gewichtete Summe, fügt einen Bias hinzu und wendet eine Aktivierungsfunktion an, bevor die Ausgabe an die nächste Schicht weitergegeben wird. Deshalb wird dieses spezielle FNN auch als Multilayer-Perzeptron bezeichnet. Jedes Neuron in den versteckten Schichten ist ein Perzeptron!

Wenn es 16 Muster gäbe, die in den Zahlen 0-9 gefunden werden könnten, wäre es am besten, eine versteckte Schicht mit 16 Neuronen zu haben. Dann könntest du eine weitere Schicht hinzufügen, um Teilmuster aus diesen Mustern zu erkennen, wieder optimal mit einer Anzahl von Neuronen, die der Anzahl der existierenden Teilmuster entspricht.

Wenn das FNN ein Bild mit der Zahl "9" als Eingabe erhält, könnte das neuronale Netz den Kreis auf einer Linie, die sich nach links biegt, erkennen. Die Neuronen, die die Informationen für diese Muster enthalten, hätten eine hohe Aktivierung, was zu einer hohen Aktivierung des Ausgabeneurons führen würde, das die Information für die Zahl "9" hält.

In der Realität erfassen die neuronalen Netze jedoch nicht immer Muster so, wie wir es erwarten würden. Das macht die Erstellung von neuronalen Netzen tatsächlich schwierig: sie so zu konstruieren, dass sie die Informationen aus den Trainingsdaten optimal aufnehmen (oder "speichern") können.

Die Ausgabeschicht

In der Ausgabeschicht werden 10 Neuronen benötigt, um die gesamte Bandbreite von zehn möglichen Zahlen als Ausgabe darzustellen (Zahlen 0-9). Jedes Neuron in dieser Schicht ist wiederum ein Perzeptron: Es empfängt Eingaben von der versteckten Schicht, berechnet die gewichtete Summe, fügt einen Bias hinzu und wendet eine Aktivierungsfunktion an. In unserem Fall würden wir die Sigmoid-Aktivierungsfunktion verwenden, die uns eine Zahl liefert, die als Prozentwert interpretiert werden kann. Nachdem die Muster in den versteckten Schichten erkannt wurden, werden einige dieser Neuronen stärker aktiviert als andere. Das Neuron in der Ausgabeschicht für die Zahl "9" könnte das Ergebnis 0,9 erhalten, was einer Wahrscheinlichkeit von 90% entspricht, dass die Eingabezahl tatsächlich eine "9" war.

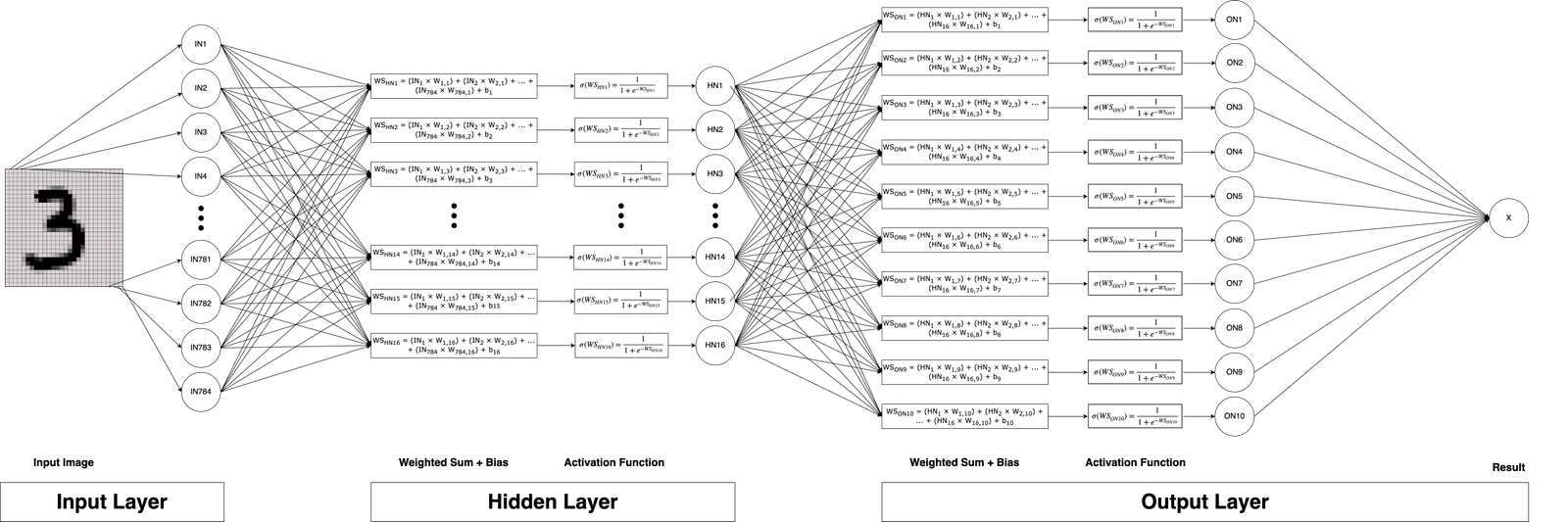
Abbildung 2: Darstellung eines Multilayer-Perzeptrons. Das Eingabebild wird in der Eingabeschicht gegeben. Die Grauwerte für jedes Pixel ergeben insgesamt 784 Merkmale. In der versteckten Schicht wird für alle 16 Neuronen die gewichtete Summe berechnet, ein Bias hinzugefügt und die Sigmoid-Aktivierungsfunktion angewendet. Das Ergebnis wird an die Ausgabeschicht weitergegeben, in der erneut für jedes der 10 Neuronen die gewichtete Summe berechnet, der Bias hinzugefügt und die Sigmoid-Aktivierungsfunktion angewendet wird. Im letzten Schritt wird das Neuron mit der höchsten Aktivierung als die im Eingabebild gegebene Zahl angesehen.

Beispiel einer Vollständigen Funktion

Ein neuronales Netzwerk ist im Wesentlichen eine hochkomplexe zusammengesetzte Funktion. Eine zusammengesetzte Funktion ist eine Funktion, die aus zwei oder mehr Funktionen besteht, wobei die Ausgabe einer Funktion zur Eingabe für die nächste wird. Diese zusammengesetzte Funktion wird dann auf einen gegebenen Eingabevektor X angewendet. Das Ergebnis der Anwendung der Funktion auf ein Neuron oder eine Schicht von Neuronen wird als Aktivierung bezeichnet. Wir wollen jedoch nicht nur die einzelnen Aktivierungen berechnen, sondern auch die Ausgabe (Vorhersage) des gesamten Netzwerks. Das Beispiel mit der Eingabe auf einem 28 × 28 Raster ist zu groß, um es vollständig aufzuschreiben, daher betrachten wir ein einfacheres, kleineres Beispiel, durch das wir ein vollständiges Verständnis dessen gewinnen können, was im neuronalen Netzwerk geschieht:

Betrachten wir die Vorhersage, ob eine Person ein Produkt kaufen wird, basierend nur auf ihrem Alter und Jahreseinkommen. Dies sind unsere zwei Eingabemerkmale. Für die versteckte Schicht werden wir zwei Neuronen haben und ein Neuron für die Ausgabeschicht. Insgesamt besteht dieses neuronale Netzwerk aus 3 Neuronen.

Für die Berechnung der Parameter haben wir:

2 × 2 + 2 für die Gewichte von der Eingabeschicht zur versteckten Schicht plus die Biases für die zwei Neuronen in der versteckten Schicht.
2 × 1 + 1 für die Gewichte von den zwei versteckten Neuronen zum Ausgabeneuron plus den Bias für das Ausgabeneuron.

Das summiert sich zu einem neuronalen Netzwerk mit 9 Parametern.

Eingabedaten:

Alter: 25 (Jahre)
Jahreseinkommen: 50 (tausend Dollar)

Gewichte & Biases:

Ich habe GPT-4o gebeten, den Code für das Training eines kleinen neuronalen Netzwerks mit PyTorch zu schreiben. GPT-4o hat dann eine Logik erstellt, um zu bestimmen, wann eine Person ein Produkt kaufen würde, und adäquate Trainingsdaten generiert, um die Konvergenz des NN zu gewährleisten. Nach 200 Epochen erreichte das NN einen Verlust von 0,6020, was für meinen Anwendungsfall ein relativ gutes Ergebnis ist. Der Verlust zeigt an, wie gut das NN konvergiert ist, wobei Werte näher an Null wünschenswerter sind. Eine Epoche bezieht sich darauf, dass das NN den gesamten Datensatz einmal verarbeitet. Bei kleinen Datensätzen wie dem in diesem Fall verwendeten liegt die Anzahl der Epochen typischerweise zwischen 100 und 1000. Folgendes sind die tatsächlichen Gewichte und Biases, die das NN während des Trainingsprozesses gelernt hat:

w_1,1 = -0,0239
w_1,2 = 0,3476
w_2,1 = -0,4298
w_2,2 = 0,30
hl_b1 = -0,0331; hl_b2 = -0,0502

Versteckte zur Ausgabeschicht:

w_1,1 = -0,1411
w_2,1 = 0,3292
ol_b1 = -0,5868

Allgemeine Struktur

Die zusammengesetzte Funktion dieses NN besteht aus zwei separaten Funktionen, die ich zur Klarheit mit unterschiedlichen Farben markieren werde:

Eingabeschicht zur versteckten Schicht:
X als Eingabe.

W₁ als Gewichte für die Verbindungen von der Eingabeschicht zur versteckten Schicht.

b₁ als Biases für die versteckte Schicht.

σ₁ (Sigma) als Aktivierungsfunktion für die versteckte Schicht.

Die Ausgabe der versteckten Schicht, H₁, kann ausgedrückt werden als:
```
H₁ = σ₁(W₁ × X + b₁)
```
Versteckte Schicht zur Ausgabeschicht:
W₂ als Gewichte von der versteckten Schicht zur Ausgabeschicht.

b₂ als Biases für die Ausgabeschicht.

σ₂ als Aktivierungsfunktion für die Ausgabeschicht.

Die Ausgabe des Netzwerks, y, kann ausgedrückt werden als:
```
y = σ₂(W₂ × H₁ + b₂)
```

Durch Kombination der beiden obigen Funktionen erhalten wir die folgende zusammengesetzte Funktion:

y(X) = σ₂(W₂ × σ₁(W₁ × X + b₁) + b₂)

Berechnung:

Bevor wir in die Berechnungen eintauchen, erinnern wir uns an die Grundlagen von Vektoren und Matrizen und deren Multiplikation.

Ein Vektor ist ein eindimensionales Array von Zahlen, dargestellt mit eckigen Klammern. Zum Beispiel:

v = [1, 2, 3]

Eine Matrix ist ein zweidimensionales Array von Zahlen, ebenfalls dargestellt mit eckigen Klammern. Zum Beispiel:

M = [[1, 2],
     [3, 4],
     [5, 6]]

Um eine Matrix mit einem Vektor zu multiplizieren, muss die Anzahl der Spalten in der Matrix gleich der Anzahl der Zeilen im Vektor sein. Der resultierende Vektor wird die gleiche Anzahl von Zeilen haben, wie die Matrix Spalten hat. Jedes Element im resultierenden Vektor wird berechnet, indem die entsprechende Zeile der Matrix mit dem Vektor multipliziert und die Ergebnisse summiert werden. Ich empfehle mal einen Blick auf die Seite http://matrixmultiplication.xyz, zu werfen, da es das Verständnis von Matrixmultiplikation erheblich erleichtert. Mathematisch wird dies ausgedrückt als:

(M × v)_i = Σ_j M_i,j × v_j

In diesem Ausdruck:

(M × v) repräsentiert den resultierenden Vektor aus der Matrix-Vektor-Multiplikation.
i ist der Index der Zeile im resultierenden Vektor.
Σ (Sigma) bezeichnet die Summierungsoperation.
j ist der Index, der durch die Spalten der Matrix und die Elemente des Vektors läuft.
M_i,j repräsentiert das Element in der i-ten Zeile und j-ten Spalte der Matrix M.
v_j repräsentiert das j-te Element des Vektors v.

Mit anderen Worten, um das i-te Element des resultierenden Vektors zu berechnen, multiplizieren wir jedes Element in der i-ten Zeile der Matrix mit dem entsprechenden Element im Vektor und summieren die Ergebnisse.

Lass uns die Berechnung mit den tatsächlichen Zahlen, die wir haben, unter Verwendung der Matrix-Vektor-Multiplikationsformel ausfüllen:

(M × v)_i = Σ_j M_i,j × v_j

In unserem Beispiel ist der Eingabevektor:

X = [25, 50]

Die Gewichtsmatrix für die versteckte Schicht ist:

W₁ = [[W_1,1, W_1,2], [W_2,1, W_2,2]]
W₁ = [[-0,0239, 0,3476], [-0,4298, 0,30]]

Um die Matrix-Vektor-Multiplikation W₁ × X zu berechnen, wenden wir die Formel für jede Zeile der Matrix an:

(W₁ × X)₁ = Σ_j W_1,j × X_j
                = W_1,1 × X₁ + W_1,2 × X₂
                = -0,0239 × 25 + 0,3476 × 50
                = 16,7825

(W₁ × X)₂ = Σ_j W_2,j × X_j
                = W_2,1 × X₁ + W_2,2 × X₂
                = -0,4298 × 25 + 0,30 × 50
                = 4,255

Das Ergebnis der Matrix-Vektor-Multiplikation ist also:

W₁ × X = [16,7825, 4,255]

Jetzt können wir mit dem Rest der Berechnung für die Aktivierung der versteckten Schicht fortfahren:

H₁ = σ₁(W₁ × X + b₁)
   = σ₁([16,7825, 4,255] + [-0,0331, -0,0502])
   = σ₁([16,7825 + (-0,0331), 4,255 + (-0,0502)])
   = σ₁([16,7494, 4,2048])

Mit der Sigmoid-Aktivierungsfunktion σ₁ haben wir die Formel:

σ(x) = 1 / (1 + e^-x)

Wir können die Aktivierungen der beiden Neuronen der versteckten Schicht berechnen:

H₁ = [σ(16,7494), σ(4,2048)]
   = [0,9999, 0,9853]

Nun berechnen wir die Aktivierung der Ausgabeschicht unter Verwendung der Ausgabe der versteckten Schicht, der Gewichte und der Biases:

y = σ₂(W₂ × H₁ + b₂)

Die Gewichtsmatrix für die Ausgabeschicht ist:

W₂ = [[W_1,1], [W_2,1]]
W₂ = [[-0,1411], [0,3292]]

Um die Matrix-Vektor-Multiplikation W₂ × H₁ zu berechnen, wenden wir die Formel an:

(W₂ × H₁)₁ = Σ_j W_1,j × H_1,j
                  = W_1,1 × H_1,1 + W_2,1 × H_1,2
                  = -0,1411 × 0,9999 + 0,3292 × 0,9853
                  = 0,1833

Jetzt können wir mit dem Rest der Berechnung für die Aktivierung der Ausgabeschicht fortfahren:

y = σ₂(W₂ × H₁ + b₂)
   = σ₂(0,1833 + (-0,5868))
   = σ₂(-0,4035)

Mit der Sigmoid-Aktivierungsfunktion σ₂ haben wir:

y = σ(-0,4035)
   = 1 / (1 + e^0,4035)
   = 0,4005

Somit beträgt die Ausgabe des neuronalen Netzwerks für den gegebenen Input [25, 50] 0,4005, was als eine Wahrscheinlichkeit von 40,05% interpretiert werden kann, dass die Person das Produkt kaufen wird. Und das war's auch schon – wir haben gerade die inneren Abläufe eines FNN von Hand berechnet!

Dieser Teil des Prozesses kann mathematisch schwer zu verstehen sein, aber er gibt dir ein klares Bild davon, was tatsächlich passiert. Es hat mir selbst eine Menge Zeit gekostet, das alles zu begreifen. Nimm dir die Zeit, es noch einmal durchzulesen. Denk darüber nach und versuche vielleicht sogar, verschiedene Eingaben für die Berechnung zu verwenden!

Obwohl unser Beispiel relativ einfach ist, lässt es sich auf ein dichtes neuronales Netzwerk jeglicher Größe anwenden.

Für dieses Buchprojekt werde ich nicht auf die Mathematik eingehen, wie neuronale Netzwerke aus Trainingsdaten lernen. Aber jetzt sollte es viel einleuchtender sein, dass während dieses Prozesses einfach die Gewichte und Biases aktualisiert werden, um den Trainingsdatensatz genauer vorherzusagen.

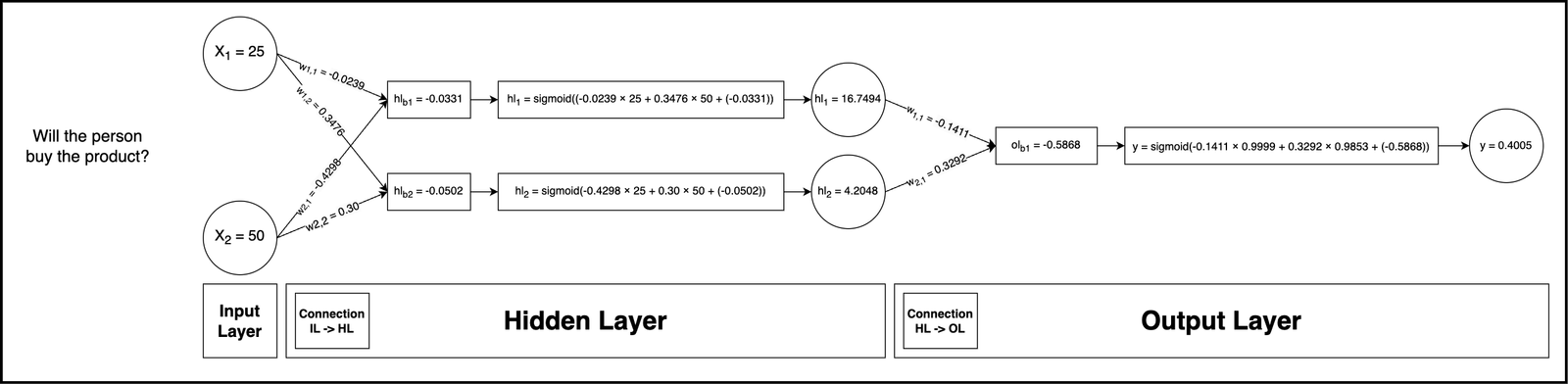
Abbildung 3: Visuelle Darstellung eines dichten neuronalen Netzwerks mit allen Berechnungen.

Für Interessierte hier die gesamte zusammengesetzte Funktion:


y(X) = σ₂([[-0.1411], [0.3292]] × σ₁([[-0.0239, 0.3476], [-0.4298, 0.30]] × X + [-0.0331, -0.0502]) + (-0.5868))

Und hier die vollständige Berechnung der Vorhersage für das neuronale Netzwerk mit dem Input [25, 50], ohne Unterbrechungen:

y(X) = σ₂(W₂ × σ₁(W₁ × X + b₁) + b₂)
     = σ₂([[W_1,1], [W_2,1]] × σ₁([[W_1,1, W_1,2], [W_2,1, W_2,2]] × X + [hl_b1, hl_b2]) + ol_b1)
     = σ₂([[-0.1411], [0.3292]] × σ₁([[-0.0239, 0.3476], [-0.4298, 0.30]] × X + [-0.0331, -0.0502]) + (-0.5868))
     = σ₂([[-0.1411], [0.3292]] × σ₁([[-0.0239, 0.3476], [-0.4298, 0.30]] × [25, 50] + [-0.0331, -0.0502]) + (-0.5868))
     = σ₂([[-0.1411], [0.3292]] × σ₁([16.7494, 4.2048]) + (-0.5868))  
     = σ₂([[-0.1411], [0.3292]] × [0.9999, 0.9853] + (-0.5868))
     = σ₂(0.1833 + (-0.5868))
     = σ₂(-0.4035)
     = 0.4005 = 40.05%

Das FNN bildet die Grundlage, um zu verstehen, wie KI-Chatbots funktionieren und wie sie auch das nächste Wort eines Satzes vorhersagen. Im nächsten Beitrag gehen wir einen Schritt weiter und betrachten die Transformer-Architektur, die das Feld der KI-gestützten Textvorhersage revolutioniert und Chatbots wie ChatGPT ermöglicht hat.

Abonniere unten, wenn du meinen Newsletter mit Updates zu Beiträgen und dem Blog erhalten möchtest (bis jetzt leider nur in Englisch verfügbar)!

Quellen & Weiterführende Literatur:

Einige Informationen und Ideen für diesen Blogbeitrag wurden mithilfe von Claude-3-Sonnet und GPT-4, KI-Assistenten entwickelt von Anthropic und OpenAI, generiert. Während Claude-3-Sonnet und GPT-4 wertvolle Vorschläge und Erklärungen lieferten, ist der hier präsentierte Inhalt das eigene Werk des Autors.