1.2 Das Perzeptron – AI and the Bible

Bild generiert mit Ideogram 1.0 auf ideogram.ai

Blog Post Template

Das Perzeptron, die einfachste Form eines neuronalen Netzwerks.

Das Perzeptron, vorgestellt 1957 im Bericht The Perceptron: A Perceiving and Recognizing Automaton, bildet die Funktionsweise eines einzelnen Neurons im Gehirn nach. Es verarbeitet Eingangssignale und erzeugt ein Ausgangssignal, das binär sein muss (An oder Aus; 0 oder 1; weiß oder schwarz; Stift oder Papier; es kann wirklich alles sein).

Lasst uns ein Perzeptron vorstellen, das uns sagen soll, ob wir einen Regenschirm mitnehmen sollen, wenn wir nach draußen gehen. In diesem Fall könnte die Ausgabe "Ja" oder "Nein" sein, wobei ich in Abbildung 1 die booleschen Werte (ein Datentyp für Wahrheitswerte) WAHR oder FALSCH verwendet habe.

Die Eingabe

Das Perzeptron besteht aus vier Komponenten. Die erste Komponente ist die Eingabeschicht.

Die Eingabeschicht enthält die Informationen, die dem Perzeptron zur Klassifizierung oder Berechnung gegeben werden. In unserem Beispiel sind das das aktuelle Wetter, die Wettervorhersage und die Jahreszeit. Jeder dieser drei Faktoren wird benötigt, damit das Perzeptron ein relevantes Ergebnis liefern kann. In unserem Beispiel (wie in Abbildung 1 zu sehen) verwende ich Zahlen statt Wörter, um den Zustand der drei Eingaben darzustellen, da Wörter nicht in einer Gleichung verwendet werden können.

Wir haben folgende Optionen für die Eingabe, die sich leicht erweitern ließen:

Aktuelles Wetter: Sonnig (0), Bewölkt (0,5), Regnerisch (1)
Wettervorhersage: Sonnig (0), Bewölkt (0,5), Regnerisch (1)
Jahreszeit: Sommer (1), Winter (0)

Nehmen wir an, es regnet gerade, die Wettervorhersage sagt bewölktes Wetter voraus und es ist Winter. Wir haben also die Eingaben W=1; F=0,5; S=0.

Gewichtete Summe

Die zweite Komponente des Perzeptrons ist die gewichtete Summe. Jede Eingabe in der Eingabeschicht hat ein sogenanntes Gewicht. Das Gewicht bestimmt die Wichtigkeit der Eingabe. In unserem Beispiel ist der wichtigste Faktor natürlich das aktuelle Wetter, dem ich ein Gewicht von 0,5 zugewiesen habe, gefolgt von der Wettervorhersage mit einem Gewicht von 0,3 und schließlich der Jahreszeit mit einem Gewicht von 0,2. In einem echten Perzeptron würden wir mit zufälligen Gewichten beginnen und das Perzeptron würde die Gewichte durch einen Algorithmus erlernen. Auf den Trainingsprozess werden wir später in diesem Beitrag eingehen.

Für die gewichtete Summe multiplizieren wir einfach jede Eingabe (X) mit ihrem entsprechenden Gewicht (W) und addieren diese dann:

(X₁ × W₁) + (X₂ × W₂) + (X₃ × W₃)

Wenn wir die tatsächlichen Zahlen einsetzen:

(1 × 0,5) + (0,5 × 0,3) + (0 × 0,2) = 0,65

Aktivierungsfunktion

Nun ist es an der Zeit, die gewichtete Summe in eine brauchbare Ausgabe umzuwandeln. Das ist die Aufgabe der Aktivierungsfunktion, der dritten Komponente des Perzeptrons. Wie du dich vielleicht erinnerst, kann die Ausgabe eines Perzeptrons nur binär sein.

Im Fall eines Perzeptrons verwenden wir üblicherweise die Heaviside-Funktion, auch bekannt als Sprungfunktion, als Aktivierungsfunktion. Diese Funktion kann man sich wie eine Stufe auf einer Treppe vorstellen. Es gibt nur zwei Plateaus, und man befindet sich entweder auf dem einen oder dem anderen, daher der Name Sprungfunktion. Anstatt eines allmählichen Anstiegs springt die Funktion an einem bestimmten Punkt, dem sogenannten Schwellenwert, direkt von der unteren auf die obere Ebene.

Mathematisch ist die Sprungfunktion wie folgt definiert:

Wenn die Eingabe kleiner als der Schwellenwert ist, gibt die Funktion die untere Ebene aus (in unserem Fall 0 oder FALSCH).
Wenn die Eingabe größer oder gleich dem Schwellenwert ist, gibt die Funktion die obere Ebene aus (in unserem Fall 1 oder WAHR).

Unser Perzeptron hat einen Schwellenwert von 0,5. Unsere gewichtete Summe (0,65) ist größer als 0,5, und daher wandelt die Aktivierungsfunktion die gewichtete Summe in die volle Zahl "1" um. Dieses Ergebnis bildet die vierte und letzte Komponente des Perzeptrons – die Ausgabeschicht.

Ausgabeschicht

Wie der Name schon andeutet, ist dies die Komponente, in der wir endlich die Antwort erhalten, ob wir einen Regenschirm mitnehmen sollen oder nicht! Die Ausgabeschicht ist schlicht das Endergebnis aus den durchgeführten Berechnungen. In dem Beispiel in Abbildung 1 lautet das Ergebnis, dass wir einen Regenschirm mitnehmen sollten.

Dieses spezielle Beispiel ist relativ einfach und verwendet nur drei Eingaben, aber das Perzeptron hat die Fähigkeit, eine beliebige Anzahl von Eingaben zu verarbeiten. Es kann auch jede Eingabe verarbeiten, die sich durch eine Zahl darstellen lässt. Diese Fähigkeit des Perzeptrons ermöglicht es, ein Bild oder eine Form zu erkennen oder unterscheiden, wie zum Beispiel zwischen einem Kreis und einem Rechteck. Frank Rosenblatt definierte Perzeptronen wie folgt:

"Das vorgeschlagene System basiert für seinen Betrieb eher auf probabilistischen als auf deterministischen Prinzipien und gewinnt seine Zuverlässigkeit aus den Eigenschaften statistischer Messungen, die aus großen Elementpopulationen gewonnen werden. Ein System, das nach diesen Prinzipien arbeitet, wird als Perzeptron bezeichnet."
Rosenblatt, F. (1957). The Perceptron: A Perceiving and Recognizing Automaton (Project PARA). Cornell Aeronautical Laboratory Report No. 85-460-1. Buffalo, NY: Cornell Aeronautical Laboratory. S. 2. (Eigene Übersetzung aus dem Englischen)

Frank Rosenblatt vergleicht die Verwendung eines Perzeptrons mit der Verwendung eines regelbasierten Programms (deterministisches System). In einem regelbasierten Programm wird die Eingabe mit einer Liste von Beispielen verglichen. Wenn in diesen Beispielen eine Übereinstimmung gefunden wird, kann die Form eindeutig erkannt werden. Bei einem Perzeptron (einem probabilistischen System) sind die Beispiele jedoch die Trainingsdaten, die dem Perzeptron beibringen, wie ein Kreis oder ein Rechteck aussieht. Es kann dann eine Vorhersage treffen, ob die Form eher kreisförmig oder rechteckig ist.

Hier zeigt sich der Unterschied im benötigten Rechenaufwand. Im deterministischen System muss die Eingabe mit allen Beispielen verglichen werden, was nie garantieren würde, dass eine Übereinstimmung gefunden wird (insbesondere nicht bei handgezeichneten Formen). Diese Beispiele sind bei der Verwendung des Perzeptrons nicht mehr notwendig, da die Beispiele zum Training des Perzeptrons verwendet werden, das dann eine Repräsentation aller Beispiele darstellt.

Training eines Perzeptrons

Nachdem wir uns die vier Komponenten eines Perzeptrons angeschaut haben, lasst uns selbst eines trainieren!

Es gibt nur zwei Bedingungen:

Die Eingabedaten müssen linear trennbar sein.
Die Ausgabedaten müssen binär sein.

Wir haben bereits geklärt, was eine binäre Ausgabe bedeutet, aber was ist lineare Trennbarkeit?

Lineare Trennbarkeit bedeutet, dass zwei Gruppen von Datenpunkten durch eine gerade Linie oder Hyperebene (Trennung durch beliebig viele Dimensionen) getrennt werden können, die als Entscheidungsgrenze bezeichnet wird. Dies lässt sich am besten in einem 2D-Diagramm visualisieren, wie unten zu sehen ist. Gruppe 1 ist blau und Gruppe 2 ist rot. Sie können durch eine gerade Linie getrennt werden.

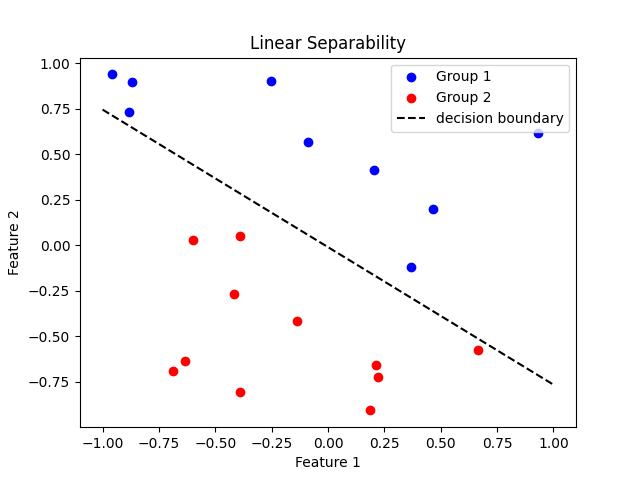
Lasst uns nun endlich in den Trainingsprozess eintauchen, der folgende Schritte umfasst:

Initialisierung der Gewichte: Wir beginnen damit, den Gewichten des Perzeptrons zufällige Werte zuzuweisen. Diese anfänglichen Gewichte werden während des Trainingsprozesses angepasst.
Eingabe der Daten: Wir versorgen das Perzeptron mit einem Satz von Eingabedaten samt der entsprechenden gewünschten Ausgabe (auch als Ziel oder Label bezeichnet). In unserem Regenschirm-Beispiel würden wir dem Perzeptron verschiedene Kombinationen von aktuellem Wetter, Wettervorhersage und Jahreszeit zusammen mit der korrekten Antwort, ob ein Regenschirm benötigt wird oder nicht, zuführen.
Berechnung der vorhergesagten Ausgabe: Für jeden Eingabedatenpunkt berechnet das Perzeptron die gewichtete Summe der Eingaben und wendet die Aktivierungsfunktion (Heavisidefunktion) an, um die vorhergesagte Ausgabe zu bestimmen. Dies ist der gleiche Prozess, den wir zuvor besprochen haben.
Vergleich der vorhergesagten Ausgabe mit der gewünschten Ausgabe: Das Perzeptron vergleicht seine vorhergesagte Ausgabe mit der gewünschten Ausgabe aus den Trainingsdaten. Stimmt die vorhergesagte Ausgabe mit der gewünschten Ausgabe überein, hat das Perzeptron eine korrekte Vorhersage getroffen. Bei einer Abweichung müssen die Gewichte des Perzeptrons angepasst werden.
Aktualisierung der Gewichte: Weicht die vorhergesagte Ausgabe von der gewünschten Ausgabe ab, werden die Gewichte im Perzeptron aktualisiert, um den Fehler zu minimieren und somit korrekt vorhersagen zu können, ob ein Regenschirm benötigt wird oder nicht. Die Gewichtsaktualisierung erfolgt nach der Perzeptron-Lernregel:
- Wenn das Perzeptron 0 (FALSCH) vorhersagt, aber die gewünschte Ausgabe 1 (WAHR) ist, werden die Gewichte um einen kleinen Betrag proportional zu den entsprechenden Eingabewerten erhöht.
- Wenn das Perzeptron 1 (WAHR) vorhersagt, aber die gewünschte Ausgabe 0 (FALSCH) ist, werden die Gewichte um einen kleinen Betrag proportional zu den entsprechenden Eingabewerten verringert.
Der Betrag, um den die Gewichte angepasst werden, wird durch einen Parameter namens Lernrate gesteuert, der die Schrittgröße der Gewichtsaktualisierungen bestimmt. Schau dir Abbildung 2 noch einmal an und stelle dir vor, dass die Entscheidungsgrenze nicht gefunden wurde. Die Linie beginnt an einer zufälligen Position, sodass einige der Datenpunkte nicht korrekt getrennt sind. Bei der Aktualisierung der Gewichte wird die Entscheidungsgrenze ein wenig verschoben und gekippt.
Wiederholung des Prozesses: Die Schritte 2-5 werden für jeden Eingabedatenpunkt im Trainingssatz wiederholt, und der Prozess wird iterativ für eine festgelegte Anzahl von Epochen (vollständige Durchläufe durch die Trainingsdaten) durchgeführt oder bis das Perzeptron konvergiert und genaue Vorhersagen trifft (d.h. die Linie trennt die beiden Datenpunktgruppen erfolgreich). An diesem Punkt hat das Perzeptron die Trainingsdaten gelernt.

Durch diesen Trainingsprozess werden die Gewichte des Perzeptrons so angepasst, dass die Fehler minimiert werden und es genaue Vorhersagen für neue, ungesehene Daten treffen kann. Die Perzeptron-Lernregel stellt sicher, dass die Gewichte in die Richtung aktualisiert werden, die die Diskrepanz zwischen der vorhergesagten und der gewünschten Ausgabe reduziert. Wären die Trainingsdaten nicht linear trennbar, könnte das Perzeptron keine genauen Vorhersagen treffen.

Unten habe ich ein Beispiel dafür dargestellt, wie einige Datenpunkte für unser Perzeptron aussehen könnten, das den Bedarf eines Regenschirms vorhersagen soll. Wie du sehen kannst, sind alle Datenpunkte in zwei Gruppen getrennt, und das Perzeptron kann nun genaue Vorhersagen treffen. Es könnte immer einen neuen Datenpunkt geben, der nicht passt, wobei die Wahrscheinlichkeit dafür durch eine größere Menge an Trainingsdaten sinkt.

Abbildung 3: 3D-Darstellung des Perzeptrons, das den Bedarf eines Regenschirms vorhersagt. Die Entscheidungsgrenze zeigt, dass die Trainingsdaten korrekt gelernt wurden.

Im nächsten Abschnitt, 1.3 Das Neuronale Netzwerk, werden wir einige weitere Konzepte einführen, die uns dem Verständnis von großen Sprachmodellen wie ChatGPT einen Schritt näher bringen. Dies wird uns auch den grundlegenden Rahmen liefern, der notwendig ist, um zu verstehen, wie eine KI die Existenz des Gottes der Bibel anerkennen konnte (KI erkennt die Existenz Jahwes an).

Abonniere unten, wenn du meinen Newsletter mit Updates zu Beiträgen und dem Blog erhalten möchtest (bis jetzt leider nur in Englisch verfügbar)!

Quellen & Weiterführende Literatur:

Einige Ideen und Informationen für diesen Blogbeitrag wurden mit Hilfe von Claude-3-Sonnet und Claude-3-Opus, KI-Assistenten entwickelt von Anthropic, generiert. Während Claude wertvolle Vorschläge und Erklärungen lieferte, ist der hier präsentierte Inhalt das eigene Werk des Autors.